👤
MANGEORGE89VIZ
a fost răspuns

Calculati raza cercului circumscris triunghiului ABC , stiind AB=3 si masura unghiului C =30°

Răspuns :

CPWVIZ
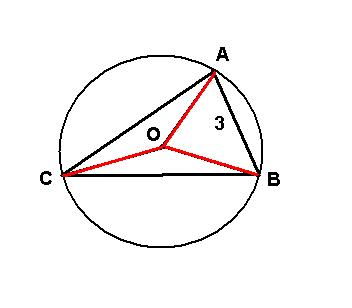
Notam cu R=raza si cu O centrul cercului si avem:

In ΔOCA, <OCA=<OAC pentru ca OC=OA=OB=R ⇒<COA=180-2*<OCA
in ΔOCB, <OCB=<OBC ot ca OC=OB=OA=R ⇒ <COB=180-2*<OCB

⇒<AOB=360-<COA-<COB=360-180+2*<OCA-180+2*<OCB
<AOB=2*<OCA+2*<OCB=2*(<OCA+<OCB)=2*30
<ACB=30=<OCA+<OCB
⇒<AOB=60°

si avem formula:
AB=2*R*sin [tex] \frac{<AOB}{2} [/tex]

3=2*R* sin (60/2)
3=2*R*sin 30°
3=2*R*1/2
3=R
Vezi imaginea CPW
Vă mulțumim pentru vizita pe platforma noastră dedicată Matematică. Sperăm că informațiile prezentate v-au fost utile. Dacă aveți întrebări sau aveți nevoie de suport suplimentar, nu ezitați să ne contactați. Așteptăm cu entuziasm să reveniți și vă invităm să ne adăugați la lista de favorite!


Viz Lesson: Alte intrebari